Navigation Part 2: Planning the gross route

Randall Maas 8/11/2012 11:53:50 AM

If we have a clear path from a starting point to the goal - that is, one that does not cross a boundary - our route planning is easy. It is just a straight line.

But what if that path crosses a boundary though?

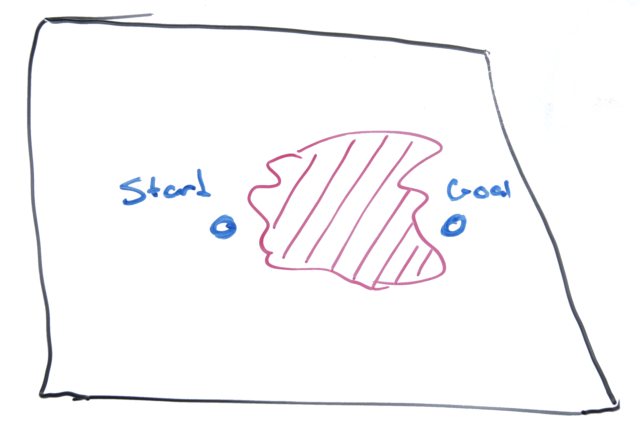
In that case, we need a more sophisticated approach.

Fortunately, Nils Nilsson told us almost everything we need to know about route planning: the A* search algorithm.

Planning a route is pretty much two parts:

Plan the big picture
Do the fine planning for the next step you have to take

We are going to create a gross (or coarse) route quickly, without a huge memory or processor load. This type of route has the advantage that it does not have to be re-planned as the bot experiences minor deviations from the ideal path.

Transforming the region into a graph

The catch is that A* works by traversing a graph. So the geographic region has to be converted into a graph, small areas that are connected logically.

The simplest method to transform the region into a graph is to

'bin' the points by dividing them a constant, and truncating the values (i.e. removing the fractional part).
The points neighboring P are the 6 surrounding points (the combination of adding -1,0, and 1 to each axis), so long as the point is in the region and the path from P to the point doesn't cross a boundary. (See the geo-fencing entry for more details)

If the region is divided into very small steps, we can skip the boundary crossing check.

To put it another way, the division constant controls how much work we do. The ideal size is coarse enough that we are only checking a handful of points to see that they are in the region (and not crossing a boundary).

If we make the grid too fine, the A* will use lots of memory and processing time to consider many small changes to the path, and we'll have to check many to see that they are in the region.
If we make the grid coarse, but not coarse enough, we will have to perform lots of region boundary crossing checks as well as checking that the point is in the region
If we make the grid too coarse, the sizing will effectively classify some small areas as not in the region when they could be used effectively.

The good news is that, unless the region tree is describing a twisty maze with lots of small passages, too coarse is a huge division value. We probably do not need to worry about it too much.

Filtering a path

Once the A* algorithm produces a path thru graph, I like to simplify it. This amounts a filtering stage to remove unnecessary waypoints. What is unnecessary?

A waypoint that is already on the path to another point
A waypoint that takes us slightly out of the way

Smoothing the path is simple:

	Take three successive points, and compute the area of the triangle
	if (area < threshold1) or 
	   (the line segment from the first to third point doesn't cross a region boundary)
	 then
		 remove the middle point

The threshold is chosen to be small enough that the path will not cross the boundary.

Making the fine route

Now that we have the coarse route, we can benefit from a more detailed route. This route isn't about being fancy. It's about shortening the distance, since the coarse route is so ... coarse.

Get the next node (P) on the coarse path
If distance between that node and the current position < threshold
```
 Remove the node from the coarse path
 Repeat from step 1
```
If there are no more points in the coarse path, return P as the fine path
Get the second node (Q) in the coarse path
Plot an A* route from the current position to the point Q, using smaller division steps
Throw out the second half of this path
Filter this path as before
Return this path as the fine route

It is very simple to use the fine path:

If fine path is empty, stop
Get next node (P) on the fine path
If distance between that node and the current position < threshold
```
 Remove the node from the coarse path
 Repeat from step 1
```
Set proximal goal as the node P

With new position information, that process is repeated.

Next time

Next time I'll look at the steering